On Thursday, we talked about confidence intervals.
A
confidence interval gives an estimated range of values which is likely to include an unknown population parameter, the estimated range being calculated from a given set of sample data.
We had this problem…
Some Senior 4 students in a large high school want to change a tradition at graduation. Instead of wearing the usual cap and gown, they want to wear formal clothes. A quick survey of 96 randomly selected students shows that 41 prefer formal wear. To answer this question, construct a “confidence interval”, most often a “95% confidence interval”.
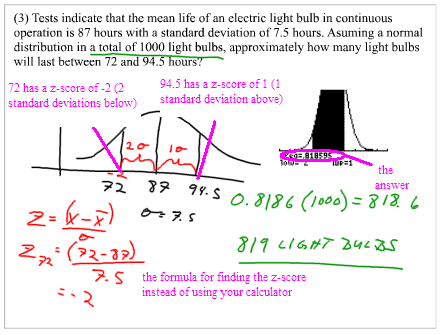
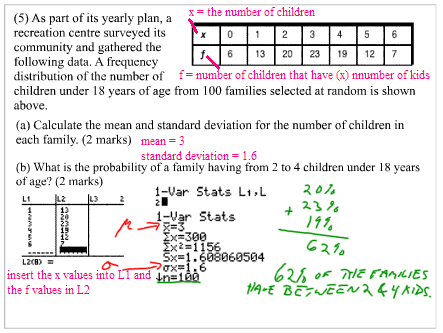
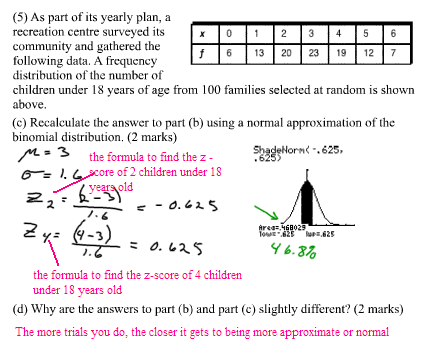
Find the probability (P), the mean (µ), and the standard deviation (σ) first.
p = 41 / 96
=
0.43µ = n ∙ p
= 96 (0.43)
=
41.28σ = √ n ∙ p ∙ (1 - p)
= √ 96 (0.43) (1 – 0.43)
= √ 23.5296
=
4.851For data that have a normal distribution with mean and standard deviation, a 95% confidence interval is:
µ ± 1.96σ
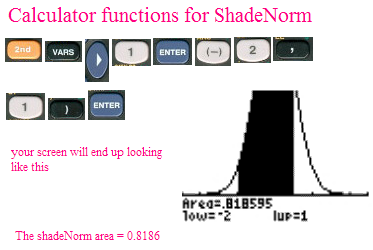
This is the range of values that lie within 1.96 standard deviations of the mean. The probability that a particular data value lies in that range is 0.95. This is shown in the graph.

95% confidence interval = µ ± 1.96σ
= 41.28 ± 1.96 (4.851)
= 41.28 ± 9.508
= 41.28 – 9.508
= 31.772
or
= 41.28 + 9.508
=
50.788We write it this way:
(31.772, 50.788)
= (31.772 / 96) × 100
=
33%= (50.788 / 96) × 100
=
53%And we write it this way:
(33%, 53%)With 95% confidence, we know that between 33% and 53% of 96 students prefer formal wear.
Now, find the Margin of Error and Percent Margin of Error.
The
margin of error is the proportion that we add to, and subtract from, the mean to construct the confidence interval.
For a 95% confidence interval:
Margin of Error = ± 1.96σ1.96 × 4.851 or
9.508 represents the half-width of the interval. This is the margin of error. To express this as a percent, we divide it by the sample size, which is 96, and multiply by 100.
% Margin of Error = ± (9.508 / 96) × 100
= ± 9.904%
Is it possible that a majority of students prefer formal wear?
** Yes, but not likely, because the high end of the 95% confidence interval is just 3% over the half of the sample size and the Margin of Error is a little bit high. When you conduct a survey, the smaller the Margin of Error, the better the results of the survey. The next scribe is Donna (",)

 To get to your TVM Solver program in your calculator, Press APPS(Applications), then press enter on Finance, and then enter on TVM Solver.
To get to your TVM Solver program in your calculator, Press APPS(Applications), then press enter on Finance, and then enter on TVM Solver.








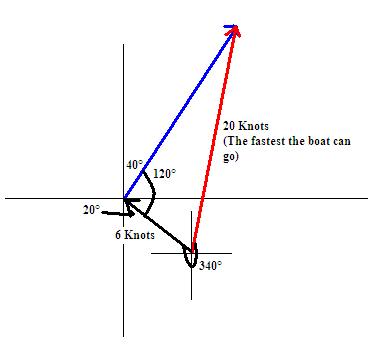
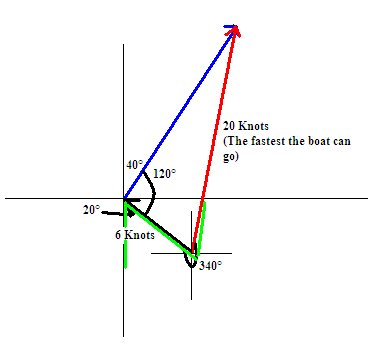
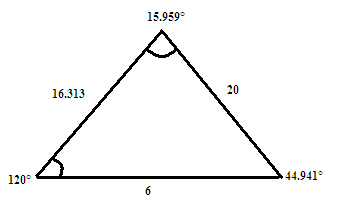


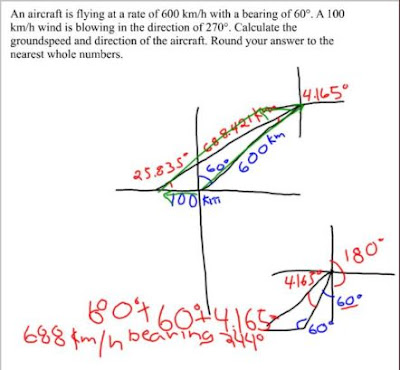







 Parallelogram
Parallelogram