You can take a sneak peak at the new blog here.
Click that picture ... there's a great article at the other end of that link.
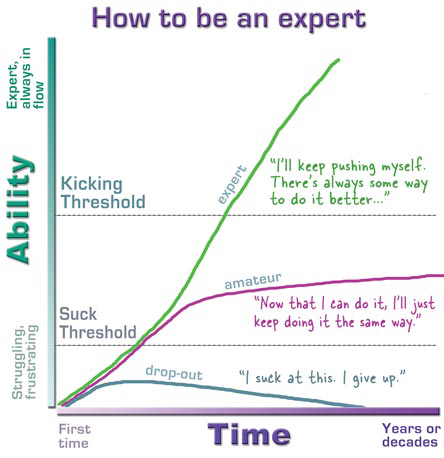
Expanding the walls of our classroom. This is an interactive learning ecology for students and parents in my Applied Math 40S class. This ongoing dialogue is as rich as YOU make it. Visit often and post your comments freely.

The teaching of mathematical concepts is the main focus of this project; so we can teach other people and learn at the same time.
Acheivement Descriptors
Instead of levels 1-4 (lowest to highest) we use these descriptors. They better describe what this project is all about.
Novice: a person who is new to the circumstances, work, etc., in which he or she is placed; a beginner.
Apprentice: to bind to or place with a master craftsman, or the like, for instruction in a trade.
Journeyperson: any experienced, competent but routine worker or performer.
Expert: possessing special skill or knowledge; trained by practice; skillful or skilled.
| Acheivement | Mathematical Challenge (25%) | Solutions (55%) | Presentation (20%) |
| Novice | Problems illustrate only an introductory knowledge of the subject. They may be unsolvable or the solutions to the problems are obvious and/or easy to find. They do not demonstrate mastery of the subject matter. | One or more solutions contain several errors with insufficient detail to understand what's going on. Explanation does not "flow," may not be in sequential order and does not adequately explain the problem(s). May also have improper mathematical notation. | Presentation may or may not include visual or other digital enhancements. Overall, a rather uninspired presentation. Doesn't really stand out. It is clear that the student has invested little effort into planning their presentation. |
| Apprentice | Problems are routine, requiring only modest effort or knowledge. The scope of the problems does not demonstrate the breadth of knowledge the student should have acquired at this stage of their learning. | One or more solutions have a few errors but are understandable. Explanation may "flow" well but only vaguely explains one or more problems. Some parts of one or more solutions are difficult to follow. May include improper use of mathematical notation. | The presentation style is attractive but doesn't enhance the content; more flashy than functional. It is clear that the student has invested some effort into planning their presentation. |
| Journeyperson | Not all the problems are "routine" in nature. They span an appropriate breadth of material. At least one problem requires careful thought such as consideration of a special case or combines concepts from more than one unit. Showcases the writer's skill in solving routine mathematical problems. | All solutions are correct and easy to understand. Very few or no minor errors. Explanation "flows" well and explains the problems step by step. Solution is broken down well and explained in a way that makes it easy to follow. May have minor use of improper mathematical notation. May point out other ways of solving one or more problems as well. | The presentation may use multiple media tools. The presentation style is attractive and maintains interest. Some of the underlying message may be lost by some aspects that are more flashy than functional. It is clear that the student has given some forethought and planning to their presentation. |
| Expert | Problems span more than one unit worth of material. All problems are non-routine. Every problem includes content from at least two different units. Problems created demonstrate mastery of the subject matter. Showcases the writer's skill in solving challenging mathematical problems. | All solutions correct, understandable and highly detailed. No errors. Explanation "flows" well, explains the problems thoroughly and points out other ways of solving at least two of them. | The presentation displays use of multiple media tools. The presentation style grabs the viewer's or reader's attention and compliments the content in a way aids understanding and maintains interest. An "eye opening" display from which it is evident that the student invested significant effort. |
Creativity (up to 5% bonus)
The maximum possible mark for this assignment is 105%. You can earn up to 5% bonus marks for being creative in the way you approach this assignment. This is not a rigidly defined category and is open to interpretation. You can earn this bonus if your work can be described in one or more of these ways:
1. A) Calculate the mean length and the standard deviation.
We found this one our calculator, by entering all our data (the 52 arrowheads) into our L1 by hitting [STAT] [1/Edit] and pinching in all 52 numbers under the L1 column. Don't forget to check your numbers just incase your numbers don't match the data. After that you hit [2nd] [QUIT] so you get back to the home screen. To get these stats you hit [2nd] [Vars] to get into your distribution menu. Then you hit [1] to get your 1-vars stats then hit [2nd] [L1] [Enter]. Your x bar is 25.44 and your σ is 5.62.
B) Determine the lengths of arrowheads one standard deviation below and one standard deviation above the mean?
In order to determine then lengths of arrowheads within 1σ below and above the mean you have to add and subtract µ from σ.
µ - σ = 19.82 (1σ below)
µ + σ = 31.06 (1σ above)
We have to find, how many arrowheads are between 20 abnd 31.
C) How many arrowheads are within one standard deviation of the mean?
In order to find how many arrowheads are between 20 and 31 you have to count how many arrowheads lie between those two numbers.
52 - 15 (the number of arrowheads that don't lie between 20 and 31) = 37.
D) What percent of the arrowheads are within one standard deviation of the mean length?
37/52 =0.7115 = 71.15%
The next question we've done before, but here's another recap..
2. A) A car designer designs car seats to fit women taller than 159.0 cm. What is the z-score of a woman who is 159.0 cm tall?
This is the formula to find the z-score. z = z-score, x = the value, µ = mean and σ = standard deviation.
159 is the value, 161.5 is the mean and 6.3 is the standard deviation.
-0.3968 is the z-score.
B) The manufacturer designs the seats to fit women with a maximum z-score of 2.8. How tall is a woman with a z-sccore of 2.8?
(z)(σ) + µ = x (this is the equation that Mr. K gave us)
To get this equation, you take the z-score equation and instead of having z by it's self, you get x by itself.
To do this, you take σ and multiply it by z, and then you take µ and move it to the other side which becomes positive, and then you get the equation (z)(σ) + µ = x.
Then you plug in the numbers into the equation:
(2.8)(6.3) + 161.5 = x
179.14 = x
Well this is the end of my scribe. Sorry it took so long. The next scribe is.. just_in.
Test Grade 55 65 75 85 95
Z-Score -2 -1 0 1 2
We then were asked which test score had a z-score of -2.76
this means which test score is -2.76 z-score from the standard deviation. The standard deviation is 75.
One way we found it ( which is completely correct )
was
Now even though that was right. It is long and messy. So mr.k taught us a faster and more efficiant way of solving the problem which is the same thing but skipping 2 of those steps.
we want to multiply the z-score we have by the standard deviation which tells us how many grades the grade we are looking for is from the mean. then subtract ( becuase the zscore was a negative number, if it were positive then we'd add) it from the mean, which will give us a score of 47.4
Our next question we were given two people, Tammy and Jamey who both applied for a job. Tammy scores 80 on her provinicial exam and the mean was 70 with a standard deviation of 4.2. Jamey score 510 on her company exam with a mean of 490 and a standard deviation of 10.3. We are to immagine that the company takes these two different exams and make them the same to figure out which one did the best. Who might get the job.
So we firgured out both girls z-scores
tammy jamey
M=70 mean 490
o=4.2 standard deviation 10.3
n=80 her score 510
80-70 510-490
4.2 10.3
=2.83 1.94
We chose Tammy because tammy's z-score was larger. This meant that she was 2.83 standard deviations ABOVE the AVERAGE of the group, where as even though jamey's test score was much HIGHER then tammy's she was only 1.94 ABOVE the average, makeing her average smaller then tammy's
Next we were asked to punch in alot of numbers in to our List1
After we placed all those numbers in our L1
we did this on our calculators
[place picture .c here]
then to draw a histogram on our calculators. If you remember we we to our plots in our calculators andturned it on then chose historgrams. The made sure our xlist was L1 and placed our frequency at 1
To do this we
Then we change our window settings to
Xmin=-6
Xmax=73
Xscl=7.4
Ymin=-10
Ymax=30
Yscl=5
Xres=1
With that we should get a graph like so
Then we were asked if it was normally distubted and we looked at the numbers that we stored.
To figure this out we looked back at the set of numbers we punched into our L1
we also looked at what we stored in S and M, which were the Mean and the standard deviation. If you remembered they were
the M = 49.06
and
the S = 7.3929
The red circled numbers are the numbers within the first deviation of the mean. We found these numbers using what we stored. Remember we stored the MEAN of the numbers we punched in and the STANDARD DEVIATION.
To find -1 of the MEAN we subtracted the S from the M like this
x-o=49.06-7.39
=41.67
then we found the +1 of the MEAN adding S to M.
x+o=49.06+7.34
=56.45
When we counted the red circles up we found 39 numbers within one deviation of the mean. That is 39 numbers our of 50 which means there are 78% of the numbers that are within the first deviation of the Mean. We decided that this was not normally distributed because the normal distribution of data within one deviation of the mean is about 68%.
The red circled.
Ok lets end it with a Mr.K joke ( for those of you who missed it! )
Whats round on the outside and high in the middle?
OHIO... OH! ahahah get it...! OHIO... great joke Mr.K
unfotunately I've run out of time so i cannot finish the second half of the classes scribe till tomarrow afternoon. But if you were wondering who the next scribe is for tomarrow its iss......... TENNYSON
( i am having a bit of problems with the spell check so ... sorry about that )




The geese who inhabit the wildlife preserve where we walk each day are back; not many, but a few as the ice begins to melt. I wonder if you see them yet, returning for spring flying along in "V" formation? Do you know what science has discovered as to why they fly that way?
FACT 1 - As each Goose flaps its wings it creates uplift for the birds that follow. By flying in a V formation, the whole flock adds 71 per cent greater flying range than if each bird flew alone.
FACT 2 - When a Goose falls out of formation, it suddenly feels the drag and resistance of flying alone. It quickly moves back into formation to take advantage of the lifting power of the bird immediately in front of it.
FACT 3 - When the lead Goose tires, it rotates back into the formation and another Goose flies to the point position.
FACT 4 - The Geese flying in formation honk to encourage those up front to keep up their speed.
FACT 5 - When a Goose gets sick, wounded or shot down, two Geese drop out of formation and follow it down to help and protect it. They stay with it until it dies or is able to fly again. Then, they launch out with another formation or catch up with the flock.
Are there lessons we can learn from a gaggle of geese? What do you think?
 Part 1 (Slide 1&2)
Part 1 (Slide 1&2)
In the Black Box--->For the calculations of the "mean" and "standard deviation" we don't use the first column in the table because it's a "range" therefore you do not know the exact number, and we use "1-VARS Stats" on our calculators.
In the Purple box---> We are looking for the number of students that have marks WITHIN the standard deviation. Within is a key word because that can mean -1 standard diviation or +1 standard deviation. So we calculate the mean + standard deviation as well as the mean - the standard deviation.
* The blue lettering means that # of students that fall in the red and green part.*
The last part---> We added the blue circled part in teh table and divided it by the numeber of students in total.
Part 2 (Slide 3)
Calculator functions for this side are:
1. Go into lists [ STAT, option 1]
2. In List 1 (L1) put in the marks. [33,42,51,60,69,78,87,96]
3. In List 2 (L2) put in number of students. [1,4,12,18,24,16,7,3]
4. Exit the screen [2nd MODE]
5. STAT > to option one "1-Var Stats" then ENTER
6. Then press 2ND #1 then the comma (,) 2ND #2 then ENTER
7.Press 2ND Y= to stat plots then press ENTER turn state plot "ON" Key down, make sure the "type" is a Histogram.
8. In "Xlist" make sure L1 is there9. In "FREQ" make sure it's L2
10. Adjust Window settings.
x-min= 29 [ Because it's the lowest mark a student can have in the table]
x-max=101 [Because we have to include the possibility of a student getting 100% on a test]
xscl=9 [Because thats the number of numbers inbetween each range]
ymin= -10 [Because we need to see all values once graphed]
ymax= 30 [Because there are 24, and you ant to show that changes at the top of the screen]
Yscl= 5
Xres=1
11. Press GRAPH
** Next we went onto dictionary slides (slide # 4-# 7)
We looked at "Standard Normal Curve" The numbers on the bottom of the curve is the standard deviation.
The numbers on the bottom of the curve is the standard deviation.
1.000 is one standard deviation above the "mean" which is 0.000
-1.000 is one standard deviation below the "mean which is 0.000
Also at the this point Mr.k mentioned an interesting fact although it has nothign to do with this topis but...
Did you know that IQ test do not really measure your intelligence?
Anyway....
Bell-shaped Curve
-Most things fall one standard deviation of the mean.
*REMINDER*
When you know the standard deviation and the mean you know the spread of how much of the mean is in each standard deviation.
Definitions:
-ZScore: Which tells how many standard deviations you are from the mean.
(Beth and Burt example)
-Six Sigma: Example most companie can't satisfiy all their customers but they try to satisfy six sigma or 99% of them, it all related back to statitics.
* The 68-95-99 rule basically describes all*
(refer to slide # 7)
Afternoon
We applied the information we learned in the morning class to real questions.
Slide #8 Questions we reffered back to the Bell shaped Curve as shown in a picture above.
a.) 358---> zscore is 2 standard deviations away from the mean
352---> z score is -4
Next we as a class put together a formula together sort of that would help us solve question b. 
Next we moved onto some more questions.
 Well that's all for me enjoy the rest of your weekend
Well that's all for me enjoy the rest of your weekendTags
The picture must be tagged properly with the course tag and assignment tag. If tags are misspelled or no tags are present the photo cannot be graded and will receive a grade of ZERO. Not tagging your photo properly and accurately is analogous to not handing in your work or not putting your name on it.
| Classification | Mathematical Content (50%) | Hot Spots (35%) | Photograph (15%) |
| Level 4 | Packed with mathematical concepts/facts. (Minimum 7 concepts/facts.) | All hot spots accessible; i.e. "smaller" hot spots are "on top" of larger ones, they do not obscure each other. All hot spots are actually labels and relate to parts of the photo (not on blank space with filled in notes). One or more hot spots include a link to a relevant supporting resource on the internet. Minimum 7 hot spots. | In focus or appropriately focused for effect. The subject of the picture occurs "naturally," it is not a contrived shot. Really makes the viewer "see" math in a place they hadn't realized it existed. (Example: trigonometry) |
| Level 3 | Significant number of concepts/facts included. (Minimum 5 concepts/facts.) | All hot spots accessible. Most hot spots are actually labels and relate to parts of the photo. Not more than one hot spot on blank space. One or more hot spots may include a link to a relevant supporting resource on the internet. Minimum 5 hot spots. | In focus or appropriately focused for effect. The subject of the photo has been "set up" or contrived yet still illustrates math found in "the real world." (Example: derivative) |
| Level 2 | Some effort to include content evident. (Minimum 3 concepts/facts.) | Most hot spots accessible. Most hot spots are actually labels and relate to parts of the photo. More than one hot spot is on "blank" space. May or may not include links to relevant supporting resource on the internet. Minimum 3 hot spots. | In focus or appropriately focused for effect. Although it is a "real world" picture, objects have been used to "draw" the math. An obviously contrived shot. (Example: trigonometry) |
| Level 1 | Very scarce content related to assignment. | Less than three hot spots are visible or have information related to the theme of the assignment. | It is evident that little effort went into finding and shooting a picture that reflects the theme of the assignment. |
| Level 0 | Content unrelated to theme of assignment. | No hot spots or mostly unrelated to the theme of the assignment. | Out of focus and/or otherwise difficult to look at. |
Creativity (up to 5% bonus)
The maximum possible mark for this assignment is 105%. You can earn up to 5% bonus marks for being creative in the way you approach this assignment. This is not a rigidly defined category and is open to interpretation. You can earn this bonus if your work can be described in one or more of these ways:



Mr. K, re-explaining about the MEAN, MEDIAN, MODE, RANGE & STANDARD DEVIATION:
Mean: Remember that mean is the "average" for the total data we calculate.
To Calculate the Mean without a calculator.
" You add up all the the numbers and divide the answer by how many numbers you have on your data"
For Example:
Data: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
1+2+3+4+5+6+7+8+9+10 = 55
55 / 10 = 5.5
So the Mean is 5.5
Median: The median in exactly in the middle.
For Example:
Data: I, 2, 3, 4, 5
1, 2, 3, 4, 5
So 3 is the Median.
Mode: The mode is the often numbers you see on your data.
For Example:
Data: 1, 2, 2, 2, 2, 3, 4, 5
So 2 is the Mode.
Range: The range is the difference between the biggest number and the smallest number on your set of data.
For Example:
Data: 1, 3, 5, 7, 8, 13
13 - 1 = 12
So 12 is the Range.
Standard deviation:
SORRY....I'll do improvements later...









This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Canada License.